Czy zdarzyło ci się kiedyś zgubić w grze? Czy aż tak bardzo zatraciłeś się w eksploracji ogromnych połaci wyrenderowanego, sztucznego terenu, że nie byłeś w stanie powrócić do punktu wyjścia? Prawdopodobnie – NIE – bo każdy współczesny tytuł z otwartym światem jest wyposażony w masę udogodnień, z pomocą których jesteśmy w stanie bez problemu uzyskać informację o swoim położeniu. Nawet pierwsze części Pokémon, mimo iż nie należały do najbardziej skomplikowanych gier, posiadały małą mapę, na której naniesiona była nasza aktualna lokalizacja. Jednak nie tylko produkcje kierowane dla dzieci ułatwiają graczowi poruszanie się po świecie. Jedna z najbardziej popularnych serii z otwartym światem (open world) – Grand Theft Auto – od pierwszej części rozpieszcza nabywców mapkami, by ci w spokoju mogli zwiedzać wirtualne miasta i wykonywać swoją robotę…

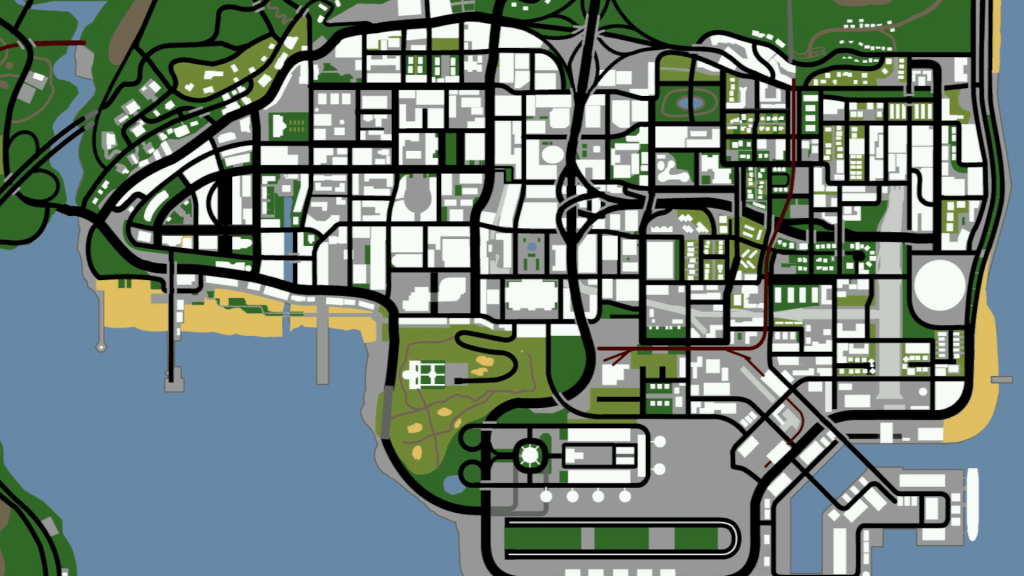
Tak… Mapy nie są jednak jedynym wirtualnym GPSem, podarowanym nam od wielmożnych twórców, by spokojnie cieszyć się poznawanym światem oraz historią. Rozwój technologii 3D, pomocnej przy generowaniu coraz to większych połaci terenu, zaowocował cichym wyścigiem pomiędzy producentami, w którym walczą między sobą o to, kto wygeneruje największą lokację. W efekcie czego z roku na rok dostajemy coraz to większe mapy, będące czasami wypełnione po brzegi treścią lub… wodą, jak miało to miejsce w przypadku Assassin’s Creed IV, gdzie lwią część terenu wypełniały morza i oceany. Fakt, czego więcej można oczekiwać od gry o piratach, prawda? Jednak większe tereny w pewien sposób wymuszają na autorach wymyślanie nowych technik ułatwiających graczowi orientację w świecie. Interesujący zabieg zastosowano między innymi w grach RPG z otwartym światem, w których odnalezienie nowych miejsc skutkuje naniesieniem odkrytych lokacji na mapę, do których można odbyć szybką podróż, skracając tym samym tułaczkę. Innym sposobem, wykorzystywanym często w grach studia Rock Star, są znaczniki wyrysowujące „najlepszą” drogę do wskazanego celu.

Nie należę do fanów eksploracji i gdy mam okazję jak najszybciej dotrzeć do celu, to preferuję trasę wyznaczoną automatycznie. Jednak podczas gry w Wiedźmina 3 zacząłem zastanawiać się nad tym, dlaczego wszystkie zaproponowane przez grę szlaki wiodą wyłącznie przez drogi, skoro bez problemu można „na skróty” przebiec przez polanę lub przepłynąć przez rzekę, zamiast tyrać do oddalonego o kilkaset metrów mostu? Problem ten nie pojawił się wyłącznie w Wieśku – spotkałem się z nim w każdym tytule, oferującym wyznaczenie optymalnej trasy do celu. W niektórych grach z otwartym światem natrafia się na inne podejście, w którym, zamiast wytyczania drogi, posiłkuje się „bezpieczniejszymi” odpowiednikami w postaci kompasu lub widocznego w HUD znacznikiem celu, tak jak ma to miejsce w przytoczonym Assassin’s Creed IV lub The Legend of Zelda: Breath of the Wild. Bezpieczniejszymi dlatego, że nienarzucana jest nam „najlepsza trasa”, powodując, że element drogi staje się po części kluczowym elementem rozgrywki. Najnowsza produkcja Hideo Kojimy – Death Stranding – zdaje się doskonale potwierdzać, że przejście z jednego punktu do drugiego, połączone z samodzielnym planowaniem, może być równie fascynujące, co walka z setką innych graczy na jednej mapie. Jednak czy gra Kojimy byłaby równie interesująca, gdyby automatycznie narzucono graczom, którą drogę mają wybrać? Dlaczego jednak nie wykorzystano wytyczania optymalnej drogi w Assassin’s Creed IV? Przecież to znacznie przyspieszałoby wykonywanie kolejnych misji. Nasuwa się więc pytanie: czy zabieg wyznaczania najszybszej drogi do celu jest podyktowany wyłącznie względami estetycznymi/artystycznymi, czy może po prostu – GRA NIE JEST W STANIE TEGO OSIĄGNĄĆ?

Przepraszam, jak tam dojadę?

Jeżeli dojeżdżasz do szkoły/uczelni lub pracy środkami komunikacji miejskiej, to prawdopodobnie masz swoją ulubioną albo najszybszą trasę na pobliski przystanek. No… chyba że znajduje się on naprzeciwko twojego domu, to nie ma o czym mówić. Istnieje jednak spora szansa, że nieustannie starasz się lub podejmowałeś kiedyś starania mające na celu optymalizację trasy, odnajdując nowe skróty, z pomocą których jesteś w stanie zaoszczędzić nieco czasu podczas porannego „spaceru”. Jednak ze względu na losowy czynnik naszego świata, nie jesteśmy w stanie do końca przewidzieć, czy uda nam się, np.: przejść przez ulicę bez zbędnego czekania lub nie natrafić na zamknięty odcinek drogi. Dlatego też, wraz z kolejnymi przejściami, uczymy się nowych zasad panujących na ścieżce – jesteśmy w stanie oszacować, kiedy zmieni się światło, w jakiej sytuacji możemy „ściąć drogę” albo kiedy przejść przez ulicę, aby skrócić czekanie na następnych światłach.

Nasz mózg doskonale analizuje zdarzenia tego typu, ucząc się ich po to, by w przyszłości skorzystać ze zdobytej wiedzy w procesie optymalizacji codziennej trasy na przystanek. Jednak dlaczego mózg sam się uczy – tak bez naszej zgody? Przecież gdyby tak cały czas potrafił, to moglibyśmy samemu nauczyć się wszystkiego w szkole, prawda?  Chyba że mielibyśmy realną potrzebę wykorzystania tej wiedzy, tak jak londyńscy taksówkarze.

Opublikowane w 2006 roku wyniki badań na londyńskich taksówkarzach oraz kierowcach autobusów udowodniły, że ludzki mózg w procesie uczenia się oraz nieustannego korzystania ze zdobytej wiedzy przechodzi zmiany strukturalne, wpływające pozytywnie na zapamiętywanie nowych informacji – nawet w starszym wieku. Osoby ubiegające się o licencję taksówkarza w Londynie muszą bowiem zdać dosyć trudny test „The Knowledge”, w którym sprawdzana jest znajomość 25000 ulic oraz 20000 punktów charakterystycznych w mieście. W badaniu sprawdzono 79-osobową grupę kandydatów na taksówkarzy, których przebadano rezonansem magnetycznym oraz sprawdzono ich zdolności w rozwiązywaniu zadań pamięciowych. Po kilku latach badania powtórzono. Osoby, które zdały The Knowledge wykazały się lepszymi zdolnościami w zapamiętywaniu punktów charakterystycznych, jednak gorszymi w odtwarzaniu skomplikowanych kształtów. Dodatkowo, po ponownym przebadaniu grupy rezonansem magnetycznym wykazano, że aktualni taksówkarze posiadają większą istotę szarą w tylnej części hipokampu (część mózgu odpowiedzialna za zapamiętywanie, pamięć długotrwałą, myślenie abstrakcyjne i emocje), a mniejszą przednią [1, 2]. Niestety gorsza pamięć wizualna to cena, jaką przyszło zapłacić taksówkarzom za całkiem sprawny proces optymalizacji trasy oraz zdolność zapamiętywania konkretnych punktów. Spokojnie, nie oznacza to jednak, że częste wycieczki spowodują, że gorzej będziecie zapamiętywać skomplikowane kształty…

…gdyż przyszło nam żyć w czasach, w których komputery wyręczają nas z większości czynności. Nie musimy więc poświęcać części swojego mózgu, jeżeli chcemy szybciej dotrzeć na przystanek. Jest na to rozwiązanie.

Komiwojażer – czyli tam i z powrotem

„A gdyby tak zoptymalizować trasy autobusów szkolnych?” – prawdopodobnie pomyślał sobie Merrilll M. Flood w 1937 roku, gdy podjął jedne z pierwszych prób praktycznego wykorzystania tzw. Problemu Komiwojażera.

Problematyka optymalizacji trasy potrzebnej do zaliczenia konkretnych punktów kontrolnych sięga już dosyć odległych czasów. Pierwsze wzmianki o tym zagadnieniu, nota bene – matematycznym, odnaleźć można już w 1832 roku, w jednym z podręczników z rozrysowaną mapką Niemiec i Szwajcarii [3, 4]. Jednak ze względu na brak matematycznego dowodu, traktowane jest to jako mała ciekawostka. Kamieniem węgielnym Problemu Komiwojażera – który oparty jest na tzw. Teorii grafów – zdaje się być sformułowanie Sir Williama Rowana Hamiltona, dotyczące problemu cyklu o długości n w n-wierzchołkowym grafie [3]. Na jego cześć został nazwany wspomniany graf, którego przykładowy wygląd możecie zobaczyć poniżej.

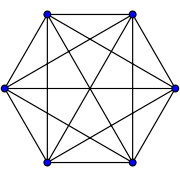
Ze względu na początki obliczeń numerycznych z wykorzystaniem komputerów dorównujących wydajnością współczesnym kalkulatorom szkolnym nie zajmowano się intensywnie Problemem Komiwojażera, gdyż w 1930 roku Karl Menger zdefiniował go jako problem o wysokiej trudności obliczeń [5]. Jednak ciężar tego zadania nie zniechęcił Merrilla M. Flooda, który nie tylko zaszczepił wśród matematyków chęć do rozwiązywania tego zagadnienia, ale i rozpowszechnił je w armii – okres ten przypadł na czas II wojny światowej – reklamując go jako doskonały sposób na rozwiązanie logistycznych problemów wojskowych [6]. Poza tym, Dr Flood uważa się za autora określenia „oprogramowanie” – to jedynie taka drobna ciekawostka do krzyżówki [7]. Dlaczego jednak zagadnienie to jest aż tak trudne? Chyba czas wyjaśnić sobie, czym w ogóle jest ten cały Problem Komiwojażera.

Komiwojażer – „przedstawiciel firmy podróżujący w celu zdobywania klientów i przyjmowania zamówień na towar” [8]. Problem Komiwojażera – ang. Travelling Salesman/Salesperson Problem (TSP) to optymalizacyjne zagadnienie matematyki, w którym tytułowy domokrążca musi zaliczyć każdy z punktów kontrolnych dokładnie raz oraz wrócić do miejsca, z którego rozpoczął podróż [3]. Zadanie jest proste – odnaleźć taką trasę, by łączny koszt przewozu lub czas (w zależności od kryteriów) był jak najmniejszy. W celu lepszej wizualizacji, przedstawiłem poniżej przykładowe rozmieszczenie miejscowości (punkty), połączonych możliwymi drogami z opisanymi odległościami. I nie – nie jest to matematyczny pentagram.

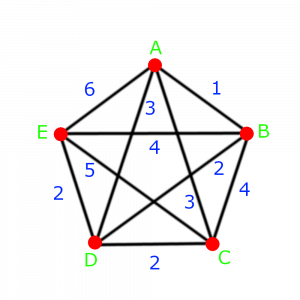
Jest to jeden z cyklów Hamiltona, o cyklu (łączna droga na zewnętrznej krawędzi) równym 15. Cały szkopuł tkwi w odnalezieniu optymalnego rozwiązania. Jak idea i założenia są banalne, to niestety sama realizacja jest już nieco bardziej złożona. Trudność ta objawia się bowiem w ilości wariantów, które należy przeanalizować, by odnaleźć rozwiązanie optymalne – najlepsze. Jeżeli rozpatrywalibyśmy przypadek, w którym nie precyzujemy, z którego miasta wyruszamy oraz nie musimy wracać do miejsca początkowego, tylko szukamy optymalnego punktu startowego oraz trasy, okazuje się, że musimy przeanalizować aż 5! przypadków. Dlaczego aż tyle? Ale zaraz… Jak się liczyło silnię(!)?

W ramach przypomnienia – silnia to wartość dowolnej liczby n, która jest równa iloczynowi kolejnych liczb naturalnych od 1 do n, tzn. n! = 1 × 2 × … × n [9]. Oznacza to, że w naszym przypadku będzie to 5 × 4 × 3 × 2 × 1, co daje łączną wartość aż 120 wariantów. Wow, to całkiem sporo. Dlaczego więc aż tyle możliwości? W omawianym przypadku, w którym nie mamy zdefiniowanego punktu startowego, początkowo dysponujemy pięcioma punktami, w następnym kroku pozostałymi czterema (w poprzednim manewrze wykorzystaliśmy już jeden), potem trzy, następnie dwie, by finalnie pozostać z jedną możliwością.

Dobra, jednak odnieśmy się do nieco bardziej praktycznego (przynajmniej z perspektywy gracza) przypadku. Załóżmy, że mamy mało czasu – za chwilę trzeba iść na pilny obiad do babci, a my wykonujemy niesamowicie interesujące zlecenie na potwora w Wiedźminie 3. Przykładowa droga – odbieramy zadanie u zleceniodawcy, zbieramy tropy w dwóch miejscach, kupujemy składniki na mikstury, naprawiamy rynsztunek, następnie walczymy z potworem i finalnie wracamy po nagrodę. Niech w tym przypadku naszymi punktami kontrolnymi będą wspomniane czynności. Czas poddać nasze zadanie optymalizacji – szczególnie może okazać się przydatna na etapie śledztwa, zbierania ziół oraz odwiedzin u kowala; po co jeździć losowo, skoro możemy wybrać najkrótszą drogę oraz dostosować kolejność czynności pod objęte kryterium? Ze względu na to, że miejsce początkowe oraz końcowe – wizyta u zleceniodawcy – jest stałe, łączna liczba kombinacji wyniesie już tylko (n-1)!, czyli 4! Daje to łącznie już tylko 24 możliwości. Zdecydowanie mniej niż 120, prawda? Ilość kombinacji można jednak jeszcze trochę zmniejszyć.

Jeżeli pieszy porusza się z prędkością 4 km/h, to w jakim czasie…

W Wiedźminie w większości zadań ukształtowanie terenu nie wpływa na prędkość poruszania się postaci – to nie Death Stranding, gdzie zanosząc ładunek tyramy pół godziny pod górę, by w drodze powrotnej zjechać z niej na desce… Ale, wracając… Ze względu na ten sam czas przejścia z punktu A do B i z B do A, można ten przykład potraktować jako symetryczny. Oznacza to więc, że ilość możliwych kombinacji wyniesie więc , czyli u nas 12. Jeżeli więc chcielibyśmy przeanalizować wszystkie możliwe kombinacje w zadaniu symetrycznym z powrotem do punktu startowego, w przypadku z pięcioma punktami kontrolnymi wystarczy przeszukać najmniejszą wartość spośród dwunastu kombinacji. Brzmi prosto, przecież takie „coś” można rozwiązać na kartce. Jednak, gdy ilość punktów kontrolnych zwiększymy sobie do dziesięciu, w rezultacie otrzymamy aż 181440 kombinacji, dla dwudziestu 6,082 × 10¹⁶. Analiza złożona z aż tak wielu możliwości trwałaby nie godzinami, lecz nawet latami. Gdybyśmy wysłali program analizujący wszystkie możliwe kombinacje tak złożonego projektu na superkomputer, którego moc obliczeniowa pozwala na wykonywania miliona permutacji na minutę problem n = 10 rozwiązałby w 1,8 sekundy, natomiast na wyznaczenie optymalnego rozwiązania dla n = 20 potrzebne by było około 40 tysięcy lat.

Ograniczenia narzucone na użytkownika, by ten nie przeciążył zbytnio komputera, znaleźć możecie w popularnej nawigacji internetowej – Google Maps. Jeżeli przyjdzie wam ochota na wyznaczenie trasy przechodzącej przez punkty kontrolne, to niestety będziecie zmuszeni do ograniczenia swojej podróży do dziesięciu miejsc charakterystycznych.

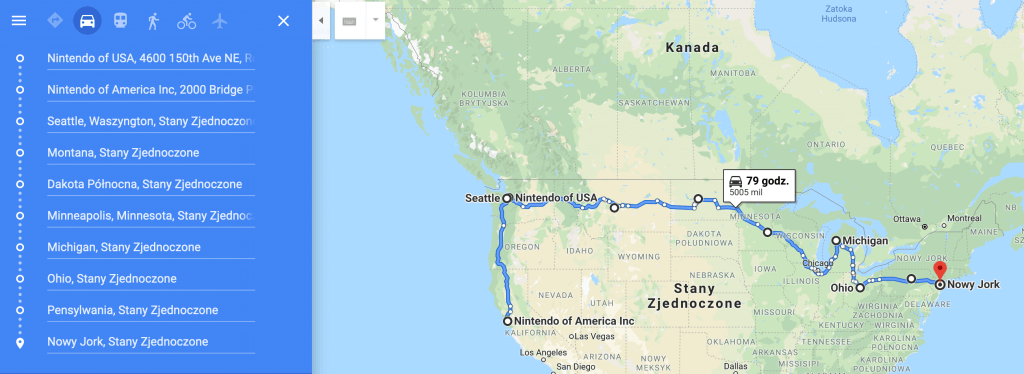
Widzicie więc, że prosty przejazd przez wybrane miejsca jest dosyć złożony obliczeniowo. Aby skrócić nieco proces optymalizacji, wymyślono szereg algorytmów dających przybliżoną wartość optymalną. Jednym z podejść jest wyszukiwanie najmniejszej wartości w każdej z kolumn tablicy rozjazdów. Rozpisaną tablicę dla omawianych pięciu miejsc zamieściłem poniżej.

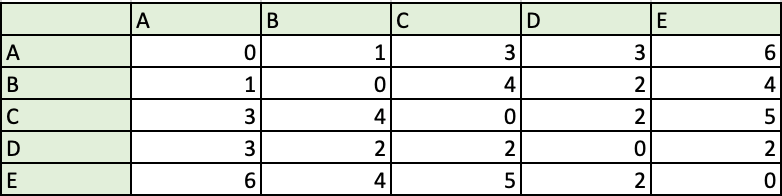
Po napisaniu programu bazującego na powyższych schemacie, uzyskałem następującą rekomendowaną trasę przejazdu. Oczywiście liczby odpowiadają kolejnym literom alfabetu łacińskiego.

Jednak by wyznaczyć optymalną drogę nie trzeba posiadać wiedzy z zakresu programowania. Wystarczy proste oprogramowanie do obsługi arkuszy kalkulacyjnych. Ja posłużyłem się Excelem. Nieco skomplikujmy sobie zadanie. Zwiększmy je do dziesięciu miast. Współrzędne punktów oraz ich rozmieszczenie w układzie współrzędnych punktów przedstawiłem na zdjęciu poniżej.

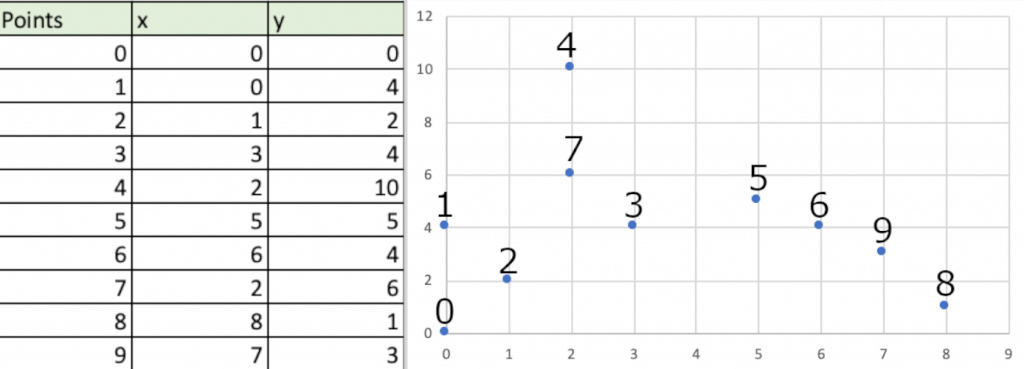
W celu wyznaczenia odległości pomiędzy punktami posłużono się twierdzeniem Pitagorasa. Obliczono odległości wzdłuż osi poziomej oraz pionowej względem następnego punktu, po czym spierwiastkowano sumę kwadratów dwóch wartości. Wynikowe wartości wpisano do tablicy rozjazdów, którą przedstawiono na rysunku poniżej.

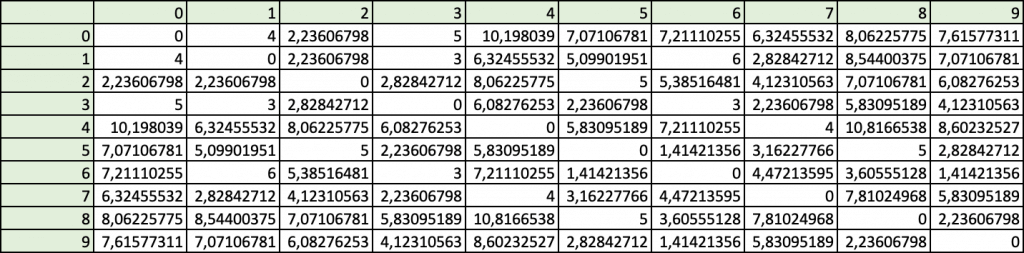
Ostatnim krokiem było uruchomienie dodatku Solver, dzięki któremu możliwe było zdefiniowanie zmiennych projektowych oraz funkcji celu zorientowanej na minimalizację drogi przejazdu. Po obliczeniach uzyskano optymalną trasę o długości 32,3955801 km oraz wyrysowano optymalną trasę przejazdu. Obliczenia te niestety nie trwały już tak krótko, jak można by się spodziewać. Mnie wyznaczenie najlepszej drogi zajęło aż 62 sekundy.

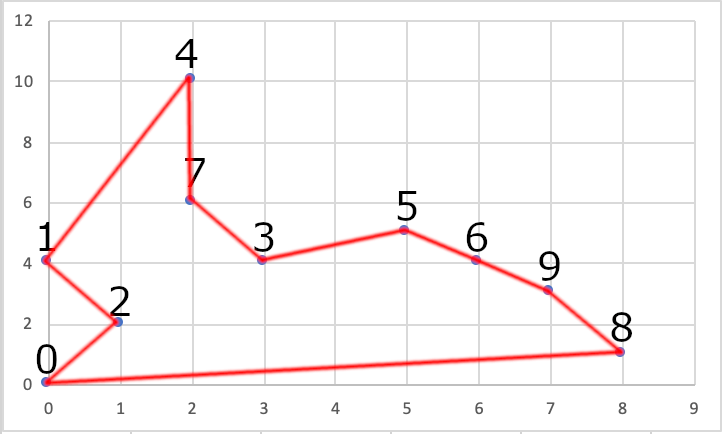
Ze względu na symetrię zagadnienia, nie ma znaczenia, czy naszą podróż zaczniemy od 0-8-9.. – 2 – 0, czy 0-2-1-..-9-8-0, gdyż uzyskamy identyczne wartości.

Zachęcam do samodzielnego spróbowania optymalizacji swojej dziennej trasy. Być może uda wam się zaoszczędzić nieco czasu.

Nie tylko chodzenie

W praktyce TSP wykorzystywane jest również do optymalizacji procesu produkcji – minimalizacja ruchów ramionami robotów, sterowanie posuwem na tokarce lub w innych metodach obróbki skrawaniem.

Mam nadzieję, że uzmysłowiłem wam złożoność problemu TSP, który towarzyszy nam na co dzień nie tylko w grach wideo, ale i prawdziwym życiu. Wróćmy jednak na Ziemię (albo do gier).

Grając w tytuły z otwartym światem jesteśmy niczym londyński taksówkarz, przygotowujący się do egzaminu The Knowledge – bacznie przyglądamy się punktom charakterystycznym, posiłkując się sporadycznie (lub częściej) mapą. Z czasem zaczynamy się powoli orientować w wirtualnej krainie; wiemy już, w którą ścieżkę skręcić, by dotrzeć do celu. Stopniowo wytwarzamy sobie własne mapy terenu, by nie raz wykorzystywać je do przeprowadzania samodzielnej optymalizacji trasy. Oczywiście nasze szybkie, podświadome kalkulacje nie należą do najdokładniejszych, gdyż, podobnie jak algorytmy wykorzystywane do rozwiązywania skomplikowanych problemów, bazujemy na przybliżeniach.

Pod tym względem zdajemy się lekko odciążać konsolę ze zbędnych obliczeń. Chyba nie grałoby się przyjemniej w The Legend of Zelda: Breath of the Wild, gdyby tytuł automatycznie wyznaczał nam optymalną trasę, uwzględniając ukształtowanie terenu i jeszcze masę innych czynników kosztem oprawy graficznej. Element samodzielnego odkrywania drogi do celu staje się więc interesującą częścią rozgrywki, pobudzającą naszą ciekawość do samodzielnego wytyczania nowych tras.

Ponownie gracze zbliżają się do wspomnianych londyńskich taksówkarzy, u których zarejestrowano zmiany w strukturze mózgu. Zwiększona aktywność w substancji białej mózgu oraz ilość połączeń w tym obszarze zauważalna jest u graczy preferujących gatunek RTS; opierający się przede wszystkim na ciągłej optymalizacji wielokryterialnej. Polscy naukowcy dowiedli, że gracze gry StarCraft II wykazują się większą wydajnością poznawczą wirtualno-przestrzenną niż inni gracze [10].

Wchodzimy więc nie tylko w interakcję ze światem gry poprzez wydawanie poleceń kontrolerem, lecz tworzymy z nim bezpośrednią więź, poddając go licznym procesom obliczeniowym. Nasz mózg jest jednak zdolny do czegoś więcej! Możemy samodzielnie wytwarzać światy, nadawać im historię i tworzyć super postacie. W połączeniu z podświadomymi obliczeniami, których wynikiem nie jest wyłącznie rozwiązywanie Problemu komiwojażera oraz własną wyobraźnią, pozwalającą na tchnienie wirtualnego życia, przewyższamy nie jeden zaawansowany superkomputer, ale i przede wszystkim ukochanego przez nas – Switcha.

Bibliografia:

[1] E.A. Magire, K. Woollett, H.J. Spiers, London taxi drivers and bus drivers:a structural MRI and neuropsychological analysis. Hippocampus. Vol 16 (12). 2006

[2] Hipokamp. Internetowy słownik języka polskiego PWN

https://sjp.pwn.pl/sjp/hipokamp;2560541 (dostęp 28.02.2020)

[3] M.M. Sysło, N. Deo, J. S. Kowalik. Algorytmy optymalizacji dyskretnej z programami w języku Pascal. Wydawnictwo naukowe PWN, 1995

[4] Problem komiwojażera. Wikipedia. https://pl.wikipedia.org/wiki/Problem_komiwoja%C5%BCera (dostęp 06.01.2020)

[5] A. Schrijver, Combinatorial Optimization: Polyhedra and Efficiency. Springer. 2003

[6] M. M. Flood, The Traveling-Salesman Problem, Operations Research. Informs. 1956

[7] Merrill M. Flood. Wikipedia https://en.wikipedia.org/wiki/Merrill_M._Flood (dostęp 12.01.2020)

[8] Komiwojażer. Internetowy słownik języka polskiego PWN https://sjp.pwn.pl/sjp/komiwojazer;2564041.html (dostęp 06.01.2020)

[9] Silnia. Internetowy encyklopadia PWN. https://encyklopedia.pwn.pl/haslo/silnia;3975225.html (dostęp 13.01.2020)

[10] N. Kowalczyk, F. Shi, M. Magnuski, M. Skorko, P. Dobrowolski, B. Kossowski, A. Marchewka, M. Bielecki, M. Kossut, A. Brzezicka. Real‐time strategy video game experience and structural connectivity – A diffusion tensor imaging study. Human Brain Mapping. Volume 39 (9). 2018. Pages 3742-3758